Steve Wyborney's Blog

Sharing Thoughts About Education

Subscribe

NYABS Part 3: Number Trading

Number Trading Comparison Pic

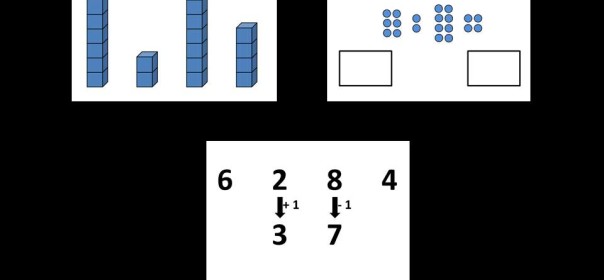
It’s possible you’ll feel that Number Trading is more like Leveling Off or that it is more like Passing Out.  Take a look at the Number Trading strategy.  You’ll understand a new way to find the mean, and then you’ll begin to wonder how these strategies are (and are not) related to one another.

This is Not Your Average Blog Series (NYABS).

 

 

Not Your Average Blog Post Series

NYABS Part 1:  Leveling Off

NYABS Part 2:  Passing Out

NYABS Part 3:  Number Trading

NYABS Part 4:  Something Familiar

NYABS Part 5:  Building the Icon Map

NYABS Part 6:  Deliberately Challenging Your Own Thinking

Please feel free to take a look at the original Finding Bedrock post, which features my beliefs about students and launched the blog.

The Animated Multiplication Table can be found here.
Thank you for helping me on my learning mission!
I’m on a mission to find my learning by giving it away!
Steve
Categories: , , ,
Tags: , , ,
Steve Wyborney Avatar

About the author

Steve Wyborney
Steve Wyborney is an award-winning teacher and instructional coach from Oregon. He is well known for his use of instructional technology and his work with mathematics and his passionate belief in the exceptional potential of every student.

4 responses to “NYABS Part 3: Number Trading”

  1. Leslie Wiggins Avatar
    Leslie Wiggins

    DEFINATELY an interesting concept. Students wld need to have a solid number sense foundation to clearly have an understanding of this concept. The first two strategies were by far easier to “see” & therefore comprehend than this one of Number Trading. I believe it is applie titled, but much more conceptionally difficult to understand.

    Reply
    1. stevewyborney@gmail.com Avatar
      stevewyborney@gmail.com

      I agree. This strategy has moved away from the tangible representations we saw in the two previous posts. This is calling for a degree of number sense that wasn’t necessary with the first two strategies. Thank you for commenting. I really appreciate it!

      Reply
  2. Maria Shkolnik Avatar
    Maria Shkolnik

    For the third method, Number Trading, you can mention that you are focusing on two numbers at a time and “taking” 1, or 20 or any number from the highest and “giving” that amount to the lowest. It’s done to three numbers at a time if needed, but mention that the sum of what’s lost by one or two must be gained by another. No “lost” numbers!

    Note: when doing an average of three, in order to get a whole number as the answer (from a teacher’s perspective) the sum of the digits has to be divisible by three. This goes into the category of “how to write problems with nice solutions” that Al Couco and our colleagues at EDC work on.

    Reply
    1. stevewyborney@gmail.com Avatar
      stevewyborney@gmail.com

      Great comments, Maria! Thank you for sharing your insights here. With the number trading strategy, it’s also interesting if a student subtracts (and adds) too large of a number. For example, if the numbers are 12 and 20, and the student adds 5 to 12 and subtracts 5 from 20, the result will be 17 and 15. The process can easily continue from that point, but it does produce a good opportunity to think more about what numbers would make the most sense to add and subtract and then wonder why that might be true. I really appreciate your thoughts about the nice solutions, too! It is interesting to dabble with number sets that aren’t quite as nice. For example, 7, 8, and 10. A student might find a pathway to 8, 8, and 9 and then wonder how to manage part of a whole number, which leads to a great discussion.

      Reply

Leave a Reply

Your email address will not be published. Required fields are marked *